Синус (sin x) и косинус (cos x) – свойства, графики, формулы. Свойства синуса, косинуса, тангенса и котангенса угла График минус косинус x

С центром в точке A .
α - угол, выраженный в радианах.

Определение
Синус (sin α) - это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

Косинус (cos α) - это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

;
;
.

;
;
.

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2 π .

Четность

Функция синус - нечетная. Функция косинус - четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n - целое).

	y = sin x	y = cos x
Область определения и непрерывность	- ∞ < x < + ∞	- ∞ < x < + ∞
Область значений	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = -1
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы

Сумма квадратов синуса и косинуса

Формулы синуса и косинуса от суммы и разности

;
;

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражение синуса через косинус

;
;
;
.

Выражение косинуса через синус

;
;
;
.

Выражение через тангенс

; .

При , имеем:
; .

При :
; .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

Выражения через комплексные переменные

;

Формула Эйлера

Выражения через гиперболические функции

;
;

Производные

; . Вывод формул > > >

Производные n-го порядка:
{ -∞ < x < +∞ }

Секанс, косеканс

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.

Арксинус, arcsin

Арккосинус, arccos

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.

Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.

В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.

Основные величины тригонометрии

Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.

В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.

Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:

Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:

Тригонометрический круг

Графически соотношение упомянутых величин можно представить следующим образом:

Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.

Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.

Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.

Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.

Углы в таблицах для тригонометрических функций соответствуют значениям радиан:

Итак, не трудно догадаться, что 2π – это полная окружность или 360°.

Свойства тригонометрических функций: синус и косинус

Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.

Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:

Синусоида	Косинусоида
y = sin x	y = cos x
ОДЗ [-1; 1]	ОДЗ [-1; 1]
sin x = 0, при x = πk, где k ϵ Z	cos x = 0, при x = π/2 + πk, где k ϵ Z
sin x = 1, при x = π/2 + 2πk, где k ϵ Z	cos x = 1, при x = 2πk, где k ϵ Z
sin x = - 1, при x = 3π/2 + 2πk, где k ϵ Z	cos x = - 1, при x = π + 2πk, где k ϵ Z
sin (-x) = - sin x, т. е. функция нечетная	cos (-x) = cos x, т. е. функция четная
	функция периодическая, наименьший период - 2π
sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk)	cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk)	cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk)
возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk]	возрастает на промежутке [-π + 2πk, 2πk]
убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk]	убывает на промежутках
производная (sin x)’ = cos x	производная (cos x)’ = - sin x

Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.

Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:

Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.

Свойства тангенсоиды и котангенсоиды

Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.

1. Y = tg x.
2. Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
3. Наименьший положительный период тангенсоиды равен π.
4. Tg (- x) = — tg x, т. е. функция нечетная.
5. Tg x = 0, при x = πk.
6. Функция является возрастающей.
7. Tg x › 0, при x ϵ (πk, π/2 + πk).
8. Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
9. Производная (tg x)’ = 1/cos 2 ⁡x .

Рассмотрим графическое изображение котангенсоиды ниже по тексту.

Основные свойства котангенсоиды:

1. Y = ctg x.
2. В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
3. Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
4. Наименьший положительный период котангенсоиды равен π.
5. Ctg (- x) = — ctg x, т. е. функция нечетная.
6. Ctg x = 0, при x = π/2 + πk.
7. Функция является убывающей.
8. Ctg x › 0, при x ϵ (πk, π/2 + πk).
9. Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
10. Производная (ctg x)’ = — 1/sin 2 ⁡x Исправить

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол - это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол - меньший 90 градусов.

Тупой угол - больший 90 градусов. Применительно к такому углу «тупой» - не оскорбление, а математический термин:-)

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника - это сторона, лежащая напротив прямого угла.

Катеты - стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим .

Синус острого угла в прямоугольном треугольнике - это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике - отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике - отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике - отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

Давайте докажем некоторые из них.

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов - свое соотношение, для сторон - свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс - их еще называют тригонометрическими функциями угла - дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .

Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

1. В треугольнике угол равен , . Найдите .

Задача решается за четыре секунды.

Поскольку , .

2 . В треугольнике угол равен , , . Найдите .

Найдем по теореме Пифагора.

Задача решена.

Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы .

Треугольник с углами и - равнобедренный. В нем гипотенуза в раз больше катета.

Мы рассмотрели задачи на решение прямоугольных треугольников - то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника . Об этом - в следующей статье.

Геометрическое определение синуса и косинуса

\(\sin \alpha = \dfrac{|BC|}{|AB|} \) , \(\cos \alpha = \dfrac{|AC|}{|AB|} \)

α - угол, выраженный в радианах.

Синус (sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AB|.

Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AC| к длине гипотенузы |AB|.

Тригонометрическое определение

С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.

На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.

Рис. 2. Тригонометрическое определение синуса и косинуса

Косинус угла - это абсцисса точки. Синус угла - это ордината точки.

На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.

Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол. На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.

Рис. 3. Синус и косинус во II, III и IV четвертях

Табличные значения синуса и косинуса

Нулевой угол \(\LARGE 0^{\circ } \)

Абсцисса точки 0 равна 1 , ордината точки 0 равна 0 . Следовательно,

cos 0 = 1 sin 0 = 0

Рис 4. Нулевой угол

Угол \(\LARGE \frac{\pi}{6} = 30^{\circ } \)

Мы видим прямоугольный треугольник с единичной гипотенузой и острым углом 30° . Как известно, катет, лежащий напротив угла 30° , равен половине гипотенузы 1 ; иными словами, вертикальный катет равен 1/2 и, стало быть,

\[ \sin \frac{\pi}{6} =\frac{1}{2} \]

Горизонтальный катет находим по теореме Пифагора (или, что то же самое, находим косинус по основному тригонометрическому тождеству):

\[ \cos \frac{\pi}{6} = \sqrt{1 - \left(\frac{1}{2} \right)^{2} } =\frac{\sqrt{3} }{2} \]

1 Почему так получается? Разрежьте равносторонний треугольник со стороной 2 вдоль его высоты! Он распадётся на два прямоугольных треугольника с гипотенузой 2, острым углом 30° и меньшим катетом 1.

Рис 5. Угол π / 6

Угол \(\LARGE \frac{\pi}{4} = 45^{\circ } \)

В данном случае прямоугольный треугольник является равнобедренным; синус и косинус угла 45° равны друг другу. Обозначим их пока через x . Имеем:

\[ x^{2} + x^{2} = 1 \]

откуда \(x=\frac{\sqrt{2} }{2} \). Следовательно,

\[ \cos \frac{\pi}{4} = \sin \frac{\pi}{4} =\frac{\sqrt{2} }{2} \]

Рис 5. Угол π / 4

Свойства синуса и косинуса

Принятые обозначения

\(\sin^2 x \equiv (\sin x)^2; \) \(\quad \sin^3 x \equiv (\sin x)^3; \) \(\quad \sin^n x \equiv (\sin x)^n \) \(\sin^{-1} x \equiv \arcsin x \) \((\sin x)^{-1} \equiv \dfrac1{\sin x} \equiv \cosec x \) .

\(\cos^2 x \equiv (\cos x)^2; \) \(\quad \cos^3 x \equiv (\cos x)^3; \) \(\quad \cos^n x \equiv (\cos x)^n \) \(\cos^{-1} x \equiv \arccos x \) \((\cos x)^{-1} \equiv \dfrac1{\cos x} \equiv \sec x \) .

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2π.

\(\sin(x + 2\pi) = \sin x; \quad \) \(\cos(x + 2\pi) = \cos x \)

Четность

Функция синус – нечетная. Функция косинус – четная.

\(\sin(-x) = - \sin x; \quad \) \(\cos(-x) = \cos x \)

Области определения и значений, экстремумы, возрастание, убывание

Основные свойства синуса и косинуса представлены в таблице (n - целое).

	\(\small < x < \)	\(\small -\pi + 2\pi n \) \(\small < x < \) \(\small 2\pi n \)
Убывание	\(\small \dfrac{\pi}2 + 2\pi n \) \(\small < x < \) \(\small \dfrac{3\pi}2 + 2\pi n \)	\(\small 2\pi n \) \(\small < x < \) \(\pi + \small 2\pi n \)
Максимумы, \(\small x = \) \(\small \dfrac{\pi}2 + 2\pi n \)	\(\small x = 2\pi n \)
Минимумы, \(\small x = \) \(\small -\dfrac{\pi}2 + 2\pi n \)	\(\small x = \) \(\small \pi + 2\pi n \)
Нули, \(\small x = \pi n \)	\(\small x = \dfrac{\pi}2 + \pi n \)
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы, содержащие синус и косинус

Сумма квадратов

\(\sin^2 x + \cos^2 x = 1 \)

Формулы синуса и косинуса суммы и разности

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \) \(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac{\pi}2 - x \right) = \sin x \) ; \(\sin\left(\dfrac{\pi}2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Формулы произведения синусов и косинусов

\(\sin x \cos y = \) \(\dfrac12 {\Large [} \sin(x - y) + \sin(x + y) {\Large ]} \)
\(\sin x \sin y = \) \(\dfrac12 {\Large [} \cos(x - y) - \cos(x + y) {\Large ]} \)
\(\cos x \cos y = \) \(\dfrac12 {\Large [} \cos(x - y) + \cos(x + y) {\Large ]} \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 {\Large [} 1 - \cos 2x {\Large ]} \)
\(\cos^2 x = \dfrac12 {\Large [} 1 + \cos 2x {\Large ]} \)

Формулы суммы и разности

\(\sin x + \sin y = 2 \, \sin \dfrac{x+y}2 \, \cos \dfrac{x-y}2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac{x-y}2 \, \cos \dfrac{x+y}2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac{x+y}2 \, \cos \dfrac{x-y}2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac{x+y}2 \, \sin \dfrac{y-x}2 \)

Выражение синуса через косинус

\(\sin x = \cos\left(\dfrac{\pi}2 - x \right) = \) \(\cos\left(x - \dfrac{\pi}2 \right) = - \cos\left(x + \dfrac{\pi}2 \right) \) \(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt{1 - \cos^2 x} \) \(\{ 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \} \) \(\sin x = - \sqrt{1 - \cos^2 x} \) \(\{ -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \} \) .

Выражение косинуса через синус

\(\cos x = \sin\left(\dfrac{\pi}2 - x \right) = \) \(- \sin\left(x - \dfrac{\pi}2 \right) = \sin\left(x + \dfrac{\pi}2 \right) \) \(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt{1 - \sin^2 x} \) \(\{ -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \} \) \(\cos x = - \sqrt{1 - \sin^2 x} \) \(\{ \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \} \) .

Выражение через тангенс

\(\sin^2 x = \dfrac{\tg^2 x}{1+\tg^2 x} \) \(\cos^2 x = \dfrac1{1+\tg^2 x} \) .

При \(- \dfrac{\pi}2 + 2 \pi n < x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac{\tg x}{ \sqrt{1+\tg^2 x} } \) \(\cos x = \dfrac1{ \sqrt{1+\tg^2 x} } \) .

При \(\dfrac{\pi}2 + 2 \pi n < x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac{\tg x}{ \sqrt{1+\tg^2 x} } \) \(\cos x = - \dfrac1{ \sqrt{1+\tg^2 x} } \) .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="Таблица синусов и косинусов" title="Таблица синусов и косинусов" ]

Выражения через комплексные переменные

\(i^2 = -1 \)
\(\sin z = \dfrac{e^{iz} - e^{-iz}}{2i} \) \(\cos z = \dfrac{e^{iz} + e^{-iz}}{2} \)

Формула Эйлера

\(e^{iz} = \cos z + i \sin z \)

Выражения через гиперболические функции

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Производные

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Вывод формул > > >

Производные n-го порядка:
\(\left(\sin x \right)^{(n)} = \sin\left(x + n\dfrac{\pi}2 \right) \) \(\left(\cos x \right)^{(n)} = \cos\left(x + n\dfrac{\pi}2 \right) \) .

Интегралы

\(\int \sin x \, dx = - \cos x + C \) \(\int \cos x \, dx = \sin x + C \)
См. также раздел Таблица неопределенных интегралов >>>

Разложения в ряды

\(\sin x = \sum_{n=0}^{\infty} \dfrac{ (-1)^n x^{2n+1} }{ (2n+1)! } = \) \(x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) \(\{- \infty < x < \infty \} \)
\(\cos x = \sum_{n=0}^{\infty} \dfrac{ (-1)^n x^{2n} }{ (2n)! } = \) \(1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) \(\{ - \infty < x < \infty \} \)

Секанс, косеканс

\(\sec x = \dfrac1{ \cos x } ; \) \(\cosec x = \dfrac1{ \sin x } \)

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.

Арксинус, arcsin

\(y = \arcsin x \) \(\left\{ -1 \leqslant x \leqslant 1; \; - \dfrac{\pi}2 \leqslant y \leqslant \dfrac{\pi}2 \right\} \)
\(\sin(\arcsin x) = x \)
\(\arcsin(\sin x) = x \) \(\left\{ - \dfrac{\pi}2 \leqslant x \leqslant \dfrac{\pi}2 \right\} \)

Арккосинус, arccos

\(y = \arccos x \) \(\left\{ -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\} \)
\(\cos(\arccos x) = x \) \(\{ -1 \leqslant x \leqslant 1 \} \)
\(\arccos(\cos x) = x \) \(\{ 0 \leqslant x \leqslant \pi \} \)

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

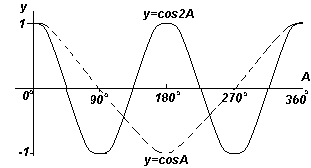
Из графиков видно что:

1. Графики синуса и косинуса колеблются в пределах между -1 и 1
2. Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90 o
3. Кривые синуса и косинуса непрерывны и повторяются с периодом 360 o , кривая тангенса имеет разрывы и повторяется с периодом 180 o .

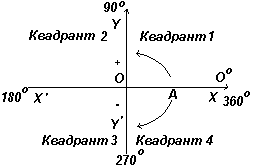На рис. слева показаны перпендикулярные оси ХХ" и YY"; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О - отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке - отрицательным.

График. Положительное или отрицательное
направление при движении по окружности.

Пусть ОА вращается против часовой стрелки таким образом, что Θ 1 - любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
Пусть ОА вращается дальше таким образом, что Θ 2 - любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Пусть ОА вращается дальше таким образом, что Θ 3 - любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .

График. Поcтроение углов в
различных квадрантах.

Пусть ОА вращается дальше таким образом, что Θ 4 - любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем - только тангенс, в четвертом только косинус, что и показано на рис. слева.

Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0 o и 360 o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin -1 , получим ответ 19,03 o . Однако существует второй угол между 0 o и 360 o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180 o - 19,03 o = 160,97 o . Таким образом, 19,03 o и 160,97 o - это углы в диапазоне от 0 o до 360 o , синус которых равен 0,3261.

Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины.

Пример 1

Найти все углы в диапазоне от 0 o до 360 o , синус которых равен -0,7071

Решение:
Углы, синус которых равен -0,7071 o находятся в третьем и четвертом квадранте, поскольку синус отрицателен в этих квадрантах (смотри рис. слева).

График. Нахождение всех углов по
заданному значению синуса (пример)

Из следующего рисунка Θ = arcsin 0,7071 = 45 o . Два угла в диапазоне от 0 o до 360 o , синус которых равен -0,7071, это 180 o +45 o =225 o и 360 o - 45 o = 315 o .

Примечание. Калькулятор дает только один ответ.
График. Нахождение всех углов по
заданному значению синуса (пример)

Пример 2

Найти все углы между 0 o и 360 o , тангенс которых равен 1, 327.

Решение:
Тангенс положителен в первом и третьем квадрантах - рис. слева.
График. Нахождение всех углов по

Из рис ниже Θ = arctg1,327= 53 o .
Два угла в диапазоне от 0 o до 360 o , тангенс которых равен 1,327, это 53 o и 180 o + 53 o , т.е. 233 o .
График. Нахождение всех углов по
заданному значению тангенса (пример)

Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o . Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30 o вертикальная составляющая - это ТS, а горизонтальная - ОS.

Из определения тригонометрических функций
sin30 o =TS/TO=TS/1, т.е. TS= sin30 o и cos30 o =OS/TO=OS/1, т.e. OS=cos30 o

Вертикальную составляющую TS можно перенести на график в виде T"S", что равно значению, соответствующему углу 30 o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.

Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева.
Из рис. слева видно, что синусоида имеет ту же форму, что и косинусоида, но смещенная на 90 o .

Периодические функции и период
Каждый из графиков функций, показанных на четырех рис. выше, повторяется при увеличении угла А, поэтому их называют периодическими функциями .
Функции y=sinA и y=cosA повторяются через каждые 360 o (или 2π радиан), поэтому 360 o называется периодом этих функций. Функции y=sin2A и y=cos2A повторяются через каждые 180 o (или π радиан),поэтому 180 o - это период для данных функций.
В общем случае если y=sinpA и y=cospA (где р - константа), то период функции равен 360 o /p (или 2π/p радиан). Следовательно, если y=sin3A, то период этой функции равен 360 o /3= 120 o , если y=cos4A, то период этой функции равен 360 o /4= 90 o .

Амплитуда
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды - 4. Аналогично для y=5cos2A амплитуда равна 5, а период - 360 o /2= 180 o .

Пример 3.
Построить y=3sin2A в диапазоне от А= 0 o до А=360 o .

Решение:
Амплитуда =3, период = 360 o /2 =180 o .

Пример 4.
Построить график y=4cos2x в диапазоне от х=0 o до х=360 o

Решение:
Амплитуда = 4. период = 360 o /2 =180 o .

Углы запаздывания и опережения
Кривые синуса и косинуса не всегда начинаются в 0 o . Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α - сдвиг фазы относительно y=sinA и y=cosA.

Составив таблицу значений, можно построить график функции y=sin(A-60 o), показанный на рис. слева. Если кривая y=sinA начинается в 0 o , то кривая y=sin(A-60 o) начинается в 60 o (т.е. ее нулевое значение на 60 o правее). Таким образом, говорят, что y=sin(A-60 o) запаздывает относительно y=sinA на 60 o .
График. y=sin(A-60 o) (синусоида).

Составив таблицу значений, можно построить график функции y=cos(A+45 o), показанный на рис. ниже.
Если кривая y=cosA начинается в 0 o , то кривая y=cos(A+45 o) начинается на 45 o левее (т.е. ее нулевая величина находится на 45 o раньше).
Таким образом, говорят, что график y=cos(A+45 o) опережает график y=cosA на 45 o .
График. y=cos(A+45 o) (косинусоида).

В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α.
Косинусоида имеет ту же форму, что и синусоида, но начинается на 90 o левее, т.е. опережает ее на 90 o . Следовательно, cosA=sin(A+90 o).

Пример 5.
Построить график y=5sin(A+30 o) в диапазоне от А=0 o до А=360 o

Решение:
Амплитуда = 5, период = 360 o /1 = 360 o .
5sin(A+30 o) опережает 5sinA на 30 o т.е. начинается на 30 o раньше.
График y=5sin(A+30 o) (синусоида).

Пример 6.
Построить график y=7sin(2A-π/3) в диапазоне от А=0 o до А=360 o .

Решение:
Амплитуда = 7, период =2π/2= π радиан
В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p , следовательно 7sin(2A-π/3) запаздывает относительно 7sin2A на (π/3)/2, т.е. на π/6 радиан или на 30 o

Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.

Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором . Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.

Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда
Т=2π/ ω (с), где
Т - это период
Число полных периодов, проходящих за 1 секунду, называется частотой f.
Частота = (количество периодов)/(секунда) = 1/ T = ω/2π Гц, т.е. f= ω/2π Гц
Следовательно, угловая скорость
ω=2πf рад/с.

Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то
А - амплитуда
ω - угловая скорость
2π/ ω - период Т, с
ω/2π - частота f, Гц
α - угол опережения или запаздывания (относительно y=Аsinωt) в радианах, он называется также фазовым углом.

Пример 7.
Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)

Решение:
i=20sin(90πt+0,26)А, следовательно,
амплитуда равна 20 А
угловая скорость ω =90π, следовательно,
период Т = 2π/ ω = 2π/ 90π = 0,022 с = 22мс
частота f = 1/Т = 1/0,022 = 45,46 Гц
фазовый угол α = 0,26 рад. = (0,26*180/π) o = 14,9 o .

Пример 8.
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α).

Решение
Амплитуда = максимальное смещение = 3м
Угловая скорость ω=2πf = 2π(55) = 110 πрад./с
Следовательно, смещение 3sin(110πt + α) м.
При t=0 смещение = 100см=1м.
Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следовательно α=arcsin0,33=19 o
Итак, смещение равно 3sin(110 πt + 0,33).

Пример 9.
Значение мгновенного напржения в схеме переменного тока в любые t секунд задается в виде v=350sin(40πt-0,542)В. Найти:
а) Амплитуду, период, частоту и фазовый угол (в градусах)
б) значение напряжения при t =0
в) значение напряжения при t =10 мс
г) время, за которое напряжение впервые достигнет значения 200 В.
Решение :
а) Амплитуда равна 350 В, угловая скорость равна ω=40π
Следовательно,
период Т=2π/ ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовый угол = 0,542 рад (0,542*180/π) = 31 o с запаздыванием относительно v=350sin(40πt)
б) Если t =0, то v=350sin(0-0,542)=350sin(-31 o)=-180,25 В
в) Если t =10 мс, то v=350sin(40π10/10 3 -0,542)=350sin(0,714)=350sin41 o =229,6 В
г) Если v=200 И, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

График. Колебательный механизм
(пример, синусоида).

v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35 o или 0,611 рад.
40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс